
Confirmed Speakers
(In Alphabetical Order)

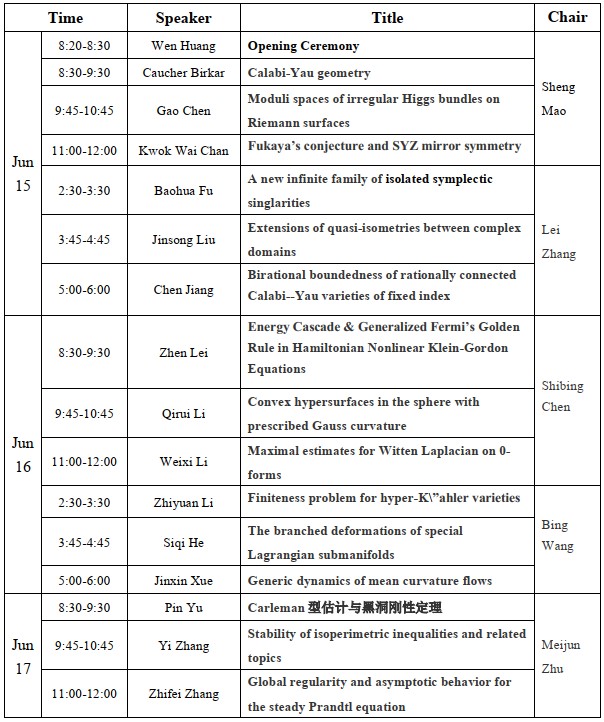
Conference Schedule
Titles & Abstracts
Caucher Birkar(Tsinghua University)
Title:Calabi-Yau geometry
Abstract:In this talk I will speak about Calabi-Yau varieties, a fundamental class of spaces in geometry. I will try to describe some results and notions, old and new.
Gao Chen(University of Science and Technology of China)
Title:Moduli spaces of irregular Higgs bundles on Riemann surfaces
Abstract:A celebrated work by Hitchin and Simpson says that there is a harmonic metric if and only if the Higgs bundle is polystable. In this talk, we restrict ourselves to Riemann surfaces. We allow the Higgs field to have isolated poles and allow the harmonic metric to have isolated conic singularities. We will show that if the dimension of the moduli space is four, then it must be ALG or ALG^*. This is a joint work with Nianzi Li.
Kwok Wai Chan (The Chinese University of Hong Kong)
Title: Fukaya’s conjecture and SYZ mirror symmetry
Abstract: The main theme of this talk is Fukaya's program on SYZ mirror symmetry. Let X be a Calabi-Yau manifold equipped with an SYZ fibration to a base manifold B. Then Fukaya's program relates holomorphic disks in X with boundaries on Lagrangian torus fibers with deformations of complex structures on the SYZ mirror, via Morse theory on the base B. I will explain joint works with Conan Leung and Ziming Ma where we proved a modified version of one of Fukaya's main conjectures.
Baohua Fu (Academy of Mathematics and Systems Science, Chinese Academy of Sciences)
Title:A new infinite family of isolated symplectic singlarities
Abstract: We construct a new infinite family of 4-dimensional isolated symplectic singularities with trivial local fundamental group, answering a question of Beauville raised in 2000. Three constructions are presented for this family: (1) as singularities in blowups of the quotient of C4by the dihedral group of order 2d, (2) as singular points of Calogero-Moser spaces associated with dihedral groups of order 2dat equal parameters, (3) as singularities of a certain Slodowy slice in the d-fold cover of the nilpotent cone in sl_d.
This is a joint work with G. Bellamy, C. Bonnaf\'e, D. Juteau, P. Levy, E. Sommers.
Jinsong Liu (Academy of Mathematics and Systems Science, Chinese Academy of Sciences)
Title: Extensions of quasi-isometries between complex domains
Abstract: In this talk, by using the Gehring-Hayman-type theorem on some complex domains, we will give some results on bi-Holder extensions not only for biholomorphisms, but also for more general Kobayashi metric quasiisometries between these domains.
Chen Jiang (Fudan University)
Title: Birational boundedness of rationally connected Calabi--Yau varieties of fixed index
Abstract: Calabi-Yau varieties are expected to satisfy certain finiteness or boundedness properties. I will discuss McKernan-Prokhorov's conjecture on the boundedness of rationally connected Calabi-Yau varieties. This conjecture is a natural generalization of the Borisov– Alexeev–Borisov (BAB) Conjecture which was solved by Birkar. I will show that the set of rationally connected Calabi--Yau varieties of fixed index of a fixed dimension is bounded modulo flops. This is a joint work with Jingjun Han.
Zhen Lei (Fudan University)
Title: Energy Cascade & Generalized Fermi’s Golden Rule in Hamiltonian Nonlinear Klein-Gordon Equations
Abstract: The Klein-Gordon equation describes relativistic spin 0 particles. We consider a Hamiltonian nonlinear Klein-Gordon equation with potential in the whole space case. Here we will show that the resonance condition leads to instability of periodic or quasi-periodic solutions in the general case including the small eigenvalue case. This resonance condition comes from a generalized Fermi’s Golden rule.
Qirui Li(Zhejiang University)
Title:Convex hypersurfaces in the sphere with prescribed Gauss curvature
Abstract:Convex hypersurfaces in the sphere with prescribed Gauss curvature was studied by many authors under the assumption of barriers or certain symmetry. We show the existence of solutions to the problem without such assumption. Multiple solutions are also discussed. The talk is based on a joint work with Qiang Guang and Xu-Jia Wang.
Weixi Li (Wuhan University)
Title: Maximal estimates for Witten Laplacian on 0-forms
Abstract: We consider the Witten Laplacian on 0-forms and obtain the maximal estimates for the Witten Laplace operator. As a result we have a new compactness criteria for resolvents of Witten Laplacian. The proof relies on the quantitative analysis on the eigenvalues of the Hessian matrix and Condition $(\Psi)$.
Zhiyuan Li (Fudan University)
Title: Finiteness problem for hyper-K\”ahler varieties
Abstract: The classical Shafarevich conjecture is about the finiteness of isomorphism classes of curves of given genus defined over a number field with good reduction outside a finite collection of places. It plays an important role in Falting’s proof of the Mordell conjecture. Similar finiteness problems arise for higher dimensional varieties. In this talk, I will talk about finiteness problems for hyper-K\”ahler varieties in arithmetic geometry. This includes the unpolarized Shafarevich conjecture for hyper-K\”ahler varieties the cohomological generalization of the Shafarevich conjecture by replacing the good reduction condition with the unramifiedness of the cohomology. I will also explain how to generalize Orr and Skorobogatov’s finiteness result on K3 surfaces to hyper-K\”ahler varieties, i.e. the finiteness of geometric isomorphism classes of hyper-K\”ahler varieties of CM type in a given deformation type defined over a number field with bounded degree. This is a joint work with Lie Fu, Teppei Takamatsu and Haitao Zou.
Siqi He (Academy of Mathematics and Systems Science, Chinese Academy of Sciences)
Title:The branched deformations of special Lagrangian submanifolds
Abstract:Special Lagrangian submanifolds are a distinguished class of real calibrated submanifolds defined in a Calabi-Yau manifold. Given a compact, smooth special Lagrangian submanifold, Mclean proved that the space of nearby special Lagrangian submanifolds could be parametrized by the harmonic 1-forms. In this talk, we will discuss some recent progress on generalizing McLean’s result to the branched deformations. We will describe how to use multi-valued harmonic functions to construct branched nearby deformations. We also discover examples of special Lagrangians that are rigid in the sense of McLean but admit branched deformations.
Jinxin Xue (Tsinghua University)
Title: Generic dynamics of mean curvature flows
Abstract: We study evolution of hypersurfaces in Euclidean spaces under mean curvature flows. The flow always develops singularities. We analyze the flow from the viewpoint of dynamical systems. In this talk, we explain how idea of global dynamics enables us to understand the behaviors of MCFs for generic initial conditions. We shall show that a generic perturbation can (1) avoid most unstable singularities, (2) give non smooth level set flow for spherical singularities and (3) isolate cylindrical singularities. This talk is based on a series of joint work with Ao Sun.
Pin Yu (Tsinghua University)
Title: Carleman型估计与黑洞刚性定理
Abstract: Carleman不等式是证明微分方程解的唯一性的常用工具。利用与波动算子相容的Carleman型估计,我们可以证明非线性波动方程的解在初始值的决定区域之外仍具有唯一性,这个想法还可以证明Kerr黑洞和Kerr-Newman黑洞的刚性。
Yi Zhang (Academy of Mathematics and Systems Science, Chinese Academy of Sciences)
Title: Stability of isoperimetric inequalities and related topics
Abstract: In 2008, Fusco, Maggi and Pratelli proved the stability of isoperimetric inequalities. Namely, for any set E\subset\mathbb R^n with |E|=|B|, one has
P(E)-P(B)\ge c(n) |E\Delta B|^2
where B is the unit ball, E\Delta B=(E\cup B)\setminus (E\cap B), and the power 2 on the right-hand side is sharp. Subsequently, Figalli, Maggi and Pratelli proved a version of this for the general Wulff perimeter. During this talk, some of recent progress in this direction will be introduced.
Zhifei Zhang (Peking University)
Title: Global regularity and asymptotic behavior for the steady Prandtl equation
Abstract: In this talk, I will introduce some results about the global $C^\infty$ regularity and asymptotic behavior for the steady Prandtl equation under favorable pressure gradient.
Supported by:Institute of Geometry and Physics & School of Mathematical Sciences, USTC
Organizers:Shibing Chen, Mao Sheng, Bin Wang
Conference Secretary:Chun Tan (nanbei0104@ustc.edu.cn), Xin Wang (xinw09@ustc.edu.cn)
Conference manual can be downloaded here: ![]() Conference Manual.pdf
Conference Manual.pdf



